LeetCode 98. Validate Binary Search Tree

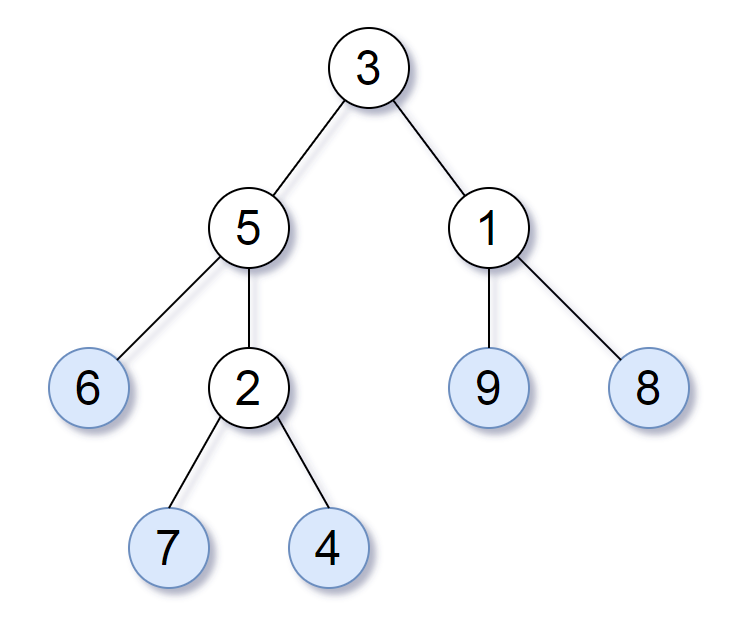
Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input:
    2
   / \
  1   3
Output: true

Example 2:

    5
   / \
  1   4
     / \
    3   6
Output: false
Explanation: The input is: [5,1,4,null,null,3,6]. The root node's value
             is 5 but its right child's value is 4.

LeetCode 200. Number of Islands.java

Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

Input:
11110
11010
11000
00000

Output: 1

Example 2:

Input:
11000
11000
00100
00011

Output: 3

LeetCode 872. Leaf-Similar Trees.java

Consider all the leaves of a binary tree.  From left to right order, the values of those leaves form a leaf value sequence.

For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

LeetCode 559. Maximum Depth of N-ary Tree.java

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

For example, given a 3-ary tree:

We should return its max depth, which is 3.

Note:

1. The depth of the tree is at most 1000.
2. The total number of nodes is at most 5000.

LeetCode 897. Increasing Order Search Tree.java

Given a tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only 1 right child.

Example 1:
Input: [5,3,6,2,4,null,8,1,null,null,null,7,9]

       5
      / \
    3    6
   / \    \
  2   4    8
 /        / \ 
1        7   9

Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

 1
  \
   2
    \
     3
      \
       4
        \
         5
          \
           6
            \
             7
              \
               8
                \
                 9  

Note:

1. The number of nodes in the given tree will be between 1 and 100.
2. Each node will have a unique integer value from 0 to 1000.

LeetCode 101. Symmetric Tree.java

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

    1
   / \
  2   2
 / \ / \
3  4 4  3

But the following [1,2,2,null,3,null,3] is not:

    1
   / \
  2   2
   \   \
   3    3

Note:
Bonus points if you could solve it both recursively and iteratively.

LeetCode 104. Maximum Depth of Binary Tree

Example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its depth = 3.

LeetCode 339. Nested List Weight Sum

https://leetcode.com/problems/nested-list-weight-sum/submissions/

Example 1:

Input: [[1,1],2,[1,1]]
Output: 10 
Explanation: Four 1's at depth 2, one 2 at depth 1.

Example 2:

Input: [1,[4,[6]]]
Output: 27 
Explanation: One 1 at depth 1, one 4 at depth 2, and one 6 at depth 3; 1 + 4*2 + 6*3 = 27.

LeetCode Weekly 124 - 995. Minimum Number of K Consecutive Bit Flips

995. Minimum Number of K Consecutive Bit Flips
In an array A containing only 0s and 1s, a K-bit flip consists of choosing a (contiguous) subarray of length K and simultaneously changing every 0 in the subarray to 1, and every 1 in the subarray to 0. Return the minimum number of K-bit flips required so that there is no 0 in the array. If it is not possible, return -1.

LeetCode Weekly 124 - 994. Rotting Oranges

994. Rotting Oranges
In a given grid, each cell can have one of three values: the value 0 representing an empty cell; the value 1 representing a fresh orange; the value 2 representing a rotten orange. Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten. Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1 instead.

LeetCode Weekly 124 - 993. Cousins in Binary Tree

993. Cousins in Binary Tree 
 In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1. Two nodes of a binary tree are cousins if they have the same depth, but have different parents. We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree. Return true if and only if the nodes corresponding to the values x and y are cousins.