Monday, September 26, 2016
Guide to Dynamic Programming - I will show the coding result.
Problem: given n, find the number of different ways to write n as the sum of 1, 3, 4
I conclude the method as 4 step solver.
Step 1. Define:
D[n] = number of ways to reach the sum n.
2. Recurrence:
D[n] = D[n - 1] + D[n - 3] + D[n - 4]
3. Base Case
D[0] = 1, D[1] = 1, D[2] = 1, D[3] = 2;
D[negative] = 0,
4. Result Case
D[n]
Time Complexity: O(n * m) - two for loops with n, m length; n is the sum; m is the length of that numbers array.
Space: O(n) - the whole D array
ok, now let's get hands dirty.
Result: [1, 1, 1, 2, 4, 6]
16:09:04:591 [main] INFO com.StandfordDP.Dynamic1 - 6
Reference: http://web.stanford.edu/class/cs97si/04-dynamic-programming.pdf
Sunday, September 25, 2016
BackPack Problems - formula + time complexity
Backpack VI
http://www.lintcode.com/problem/backpack-vi/
这题感觉就是一维的,我也是想了想整两维反而整不出来。
最后解了一维方程如下:
I. ret[i] += ret[i - nums[j - 1]];
II. time complexity还是二维的是O(m * n)
因为每次都可以取任一个数,各种反复取,而且最恶心一点是排列组合顺序不同都要算上。
所以不能直接加,而要用for循环加
外层是m或者说target
内层循环是n
所以time complexity是O(m * n)
Saturday, September 24, 2016
Recommender System
I. Introduction.
core trick - CF - based on similarity
Two CFs -
1. User CF
2. Item CF
Applications - amazon commodities/ netflix movies.
For now, let's talk about movie.
User CF - based on user similarity
Item CF - based on item similarity

Let's use item CF dude,
item have less unique quantities.
items' properties seldom change.
you like marval ant's man, i present you the iron man, sounds convincing.
II. Procedures
1. co-occurrence matrix
2. rating matrix
3. matrix computation to get recommendation result.
Ok, how to tell the similarity between different movies?
I suggest using machine learning e.g. logistic regression -
and that requires feature -
1. users
watching history
rating history
favorite list
2.
movies category
movies
Let's brainstorm -
e.g. if one user rated two movies, these two are related.
calc
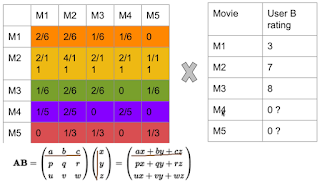
value(M1, M2) = count(x_M1 && x_M2) = 2
Rated Matrix
How about ratings?
Rating Matrix
Q&A
Q: 为什么没看过rating就是0?
A: 这个地方可以改进, 没看过, rating 可以给一个平均分
Q: 例如说来了个新用户小白,他的列全是零
Q: 用户没看过的电影rating给0分会不会影响第一个相似性矩阵的真实性? A: 会的。 一般一个更好的做法是 给没看过的电影系统平均分
Logistic regression -> Deep learning.
I. Introduction.
core trick - CF - based on similarity
Two CFs -
1. User CF
2. Item CF
Applications - amazon commodities/ netflix movies.
For now, let's talk about movie.
User CF - based on user similarity
Item CF - based on item similarity

Let's use item CF dude,
item have less unique quantities.
items' properties seldom change.
you like marval ant's man, i present you the iron man, sounds convincing.
II. Procedures
1. co-occurrence matrix
2. rating matrix
3. matrix computation to get recommendation result.
Ok, how to tell the similarity between different movies?
I suggest using machine learning e.g. logistic regression -
and that requires feature -
1. users
watching history
rating history
favorite list
2.
movies category
movies
Let's brainstorm -
e.g. if one user rated two movies, these two are related.
calc
value(M1, M2) = count(x_M1 && x_M2) = 2
Rated Matrix
How about ratings?
Rating Matrix
Normalization
Conditional probability matrix not symmetrical
没看过, rating 可以给一个平均分
Q&A
Q: 为什么没看过rating就是0?
A: 这个地方可以改进, 没看过, rating 可以给一个平均分
Q: 例如说来了个新用户小白,他的列全是零
Q: 用户没看过的电影rating给0分会不会影响第一个相似性矩阵的真实性? A: 会的。 一般一个更好的做法是 给没看过的电影系统平均分
Logistic regression -> Deep learning.
Subscribe to:
Comments (Atom)